
*Por Alex Lattaro, cientista de dados da Ilumeo
Não é novidade ouvirmos que a Ciência de Dados vem revolucionando o mercado e a maneira como as empresas enxergam suas estratégias. Porém, para algumas empresas, ainda é difícil enxergar essa aplicação ao seu negócio, seja por falta de conhecimento em ciência de dados ou até mesmo por entender que essa tecnologia não se aplica ao seu negócio devido as particularidades dele.
Bom, todo negócio tem particularidades, e essas particularidades não devem excluir você do mundo da tecnologia. Por isso, vamos fazer uma metáfora aqui com algo que todo mundo conhece pelo menos por cima, que é o futebol. Se dá para enxergar data science nesse esporte, certamente dá para enxergar no seu negócio também.
Paixão nacional
Futebol é uma paixão nacional, e se você fizer uma rápida pesquisa vai descobrir que ciência de dados já está sendo utilizada por grandes times há algum tempo. Aqui no próprio blog da Ilumeo, nós já falamos como o Liverpool utiliza da ciência de dados para interpretar a probabilidade de marcar um gol de acordo com as ações de seus jogadores dentro de campo.
Um projeto chamado Statathlon fornece relatórios para times de basquete e futebol, para que eles alcancem os resultados esperados. Como forma de divulgar seu trabalho, eles mantêm um Power BI online em que é possível observar as análises das partidas.
Dentro dessas análises eles têm como características “Attack”, “Defense”, “Set Pieces” e “Discipline”. Esse pequeno set de parâmetros são algumas das variáveis utilizadas que ajudam a calcular a probabilidade do resultado de uma partida. Por exemplo, se você acompanhou a Eurocopa, eles chegaram no seguinte resultado na disputa entre Bélgica e Portugal:

Figura 1: Uefa Euro 2020. Fonte: https://statathlon.com/
Existem muitas formas de se fazer o que eles propõem, mas vamos imaginar que eles estão usando uma regressão linear. Muito provavelmente essas 4 variáveis são os valores de beta da função deles. Abaixo vocês podem entender o funcionamento básico de uma regressão linear.

Figura 2: regressão linear. Fonte: https://datacadamia.com/

Figura 3. Equação da regressão linear. Fonte: https://towardsdatascience.com/
De uma maneira um tanto quanto simplória, podemos explicar que os Betas são as variáveis independentes responsáveis pelo valor da variável resposta, ou, variável dependente. No caso do futebol, quanto maiores os valores daquela variável, maior a chance daquele time ser vencedor da partida.
De Para…
Então, vamos colocar esse exemplo lado a lado com mercados tão diferentes como um pequeno foodtruck ou uma grande montadora de carros.

Tabela 1: Indústria versus índices
Pensando agora no caso do Food Truck. Seria possível traçar um modelo assim? Você pode pensar, mas eu nem tenho dados suficientes, não possuo uma infraestrutura com big data e tantas outras buzz words que são ditas por aí. E talvez isso seja verdade, mas não ter os dados hoje não significa que você não possa passar a tê-los amanhã.
Você poderia, por exemplo, contar quantos e quais lanches são vendidos por hora (set pieces). Aqui já teremos um bom dataset para começarmos a brincar (hora, lanche, ingredientes). Tendo quais e quanto lanches são vendidos por hora, você já consegue identificar os melhores horários de trabalho e economizar dinheiro e tempo. Também vai conseguir saber quais dias da semana você vende mais e quais os ingredientes não podem faltar.
Mas podemos ir além. Você pode, por exemplo, conhecer o seu público. Se conseguir, por exemplo, fazer um questionário de satisfação, e assim, conseguir anotar a idade dos clientes que consomem os lanches, talvez seja possível traçar uma predileção de lanche por faixa etária (criando uma estratégia de ataque para o seu time), possibilitando uma estratégia de nova alocação do seu caminhão (criando uma estratégia de defesa). Se abastecendo com o lanche do tipo X na porta de uma faculdade na hora Z.
Essa possibilidade de compra “casada” acima, lanche X na porta da faculdade Z, é um dos primeiros casos estudados em ciência de dados, quando supermercados perceberam que normalmente quem compra fralda, compra cerveja, (Cheers!)
Não se esqueça: até que se prove o contrário, são apenas hipóteses
Todas essas possibilidades que falamos em relação ao Food Truck até agora são as chamadas hipóteses, que com o auxílio da ciência de dados podem ser provadas ou refutadas. Nesse sentido, ciência de dados não pode ser confundida com advocacia de dados. Muitas vezes a hipótese que você tem é falsa, e é esplêndido aprender sobre isso, pois faz com que você pare de aplicar a mesma estratégia que não funciona.
E é por isso que tudo isso que estamos imaginando até aqui precisa ser modelado por meio de equações matemáticas. Somente assim conseguiremos sair do campo do achismo e entrarmos no campo da ciência.
Modelagem matemática
Como falado acima, chegou a hora de aplicarmos modelagens matemáticas em nosso problema. Para isso, vamos usar o exemplo das montadoras de carro.
Imagine que temos uma tabela contendo carros de várias marcas, algumas características e o preço sugerido pelo fabricante.
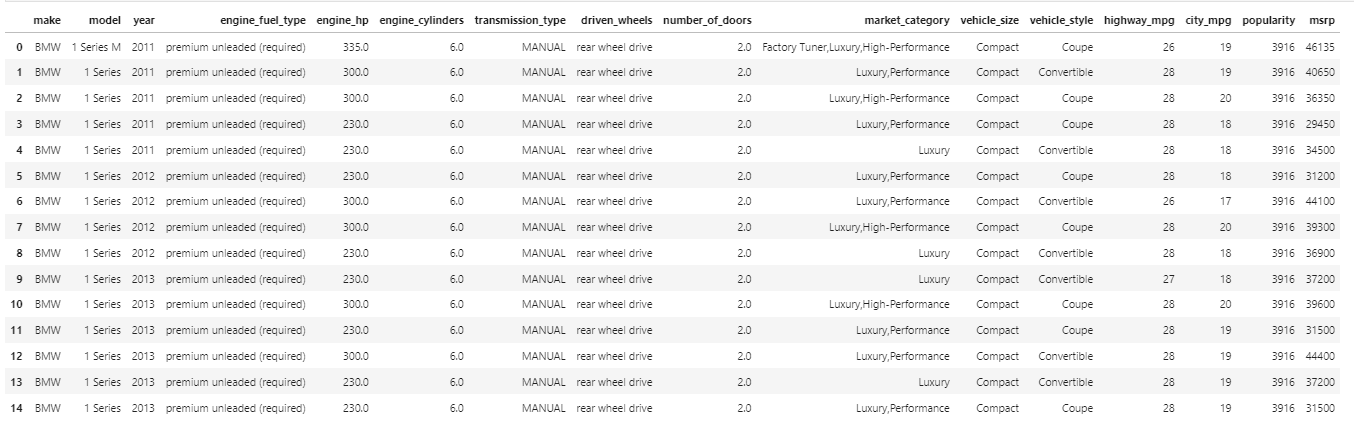
Figura 4: Base de dados Car Feature
Agora imagine que nosso objetivo seja criar uma fórmula matemática capaz de calcular o preço sugerido de um carro, baseado nas características dele. Vamos partir do caminho mais simples e tentar aplicar uma regressão linear (a fórmula que vimos acima). Quais deveriam ser nossos betas? Qual o índice de cada beta?
Antes de pensarmos nisso, podemos imaginar quais dessas variáveis (características do carro) são as mais importantes. Vamos primeiramente olhar apenas para as variáveis numéricas.
· Ano do carro
· Potência do motor
· Quantidade de cilindros
· Número de portas
· Consumo de combustível na estrada
· Consumo de combustível na cidade
· Popularidade
Você tem alguma sugestão? Será que um carro 4 portas é mais caro que um carro de duas portas? Ou melhor, qual a importância da quantidade de portas de um carro no seu valor final? Cada sugestão, dúvida ou questionamento que você tiver sobre o assunto, vamos passar a chamar de hipóteses.
Uma outra hipótese pode ser que a popularidade tem grande influência no valor do carro. Bom, vamos testar algumas?
Como um primeiro passo, podemos testar um modelo de feature importance utilizando uma floresta randômica em cima dessas variáveis numéricas.
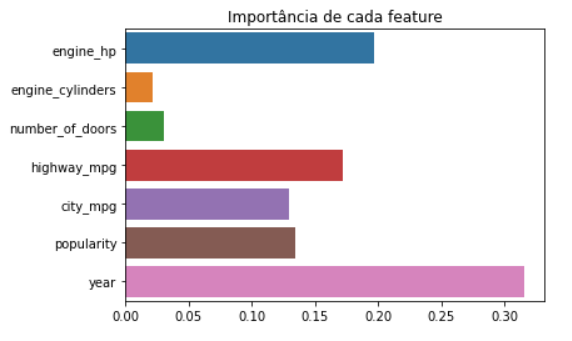
Figura 5: Feature Importance
Esse gráfico nos mostra que as características que mais influenciam no valor de um carro são o ano (year), a potência do motor (engine_hp) e o consumo de combustível na estrada (Highway_mpg). Esse simples modelo já começa a nos dar indícios de que a quantidade de portas do carro é um fator quase que irrelevante no preço final. O que nos deixa tentados a refutar essa hipótese.
É nesse momento que alguém da equipe vai chegar e dizer, “Eu acho que o tamanho do carro é mais importante que tudo isso, e ele não está contemplado no modelo”. E esse momento é ótimo, pois quanto mais ideias, melhor.
O problema é que essa variável é categórica e não numérica. Para resolver isso basta tratarmos ela como numérica.

A única ação que tivemos foi transformar “Compact” em “1” e assim por diante. Aplicando nosso modelo de floresta randômica em cima dessa transformação de dados, temos o seguinte gráfico.
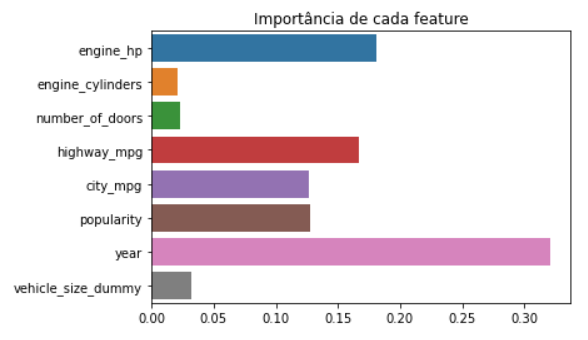
Podemos ver no gráfico que a hipótese do nosso colega foi refutada. O que é ótimo, pois agora temos uma afirmação científica e não uma sugestão.
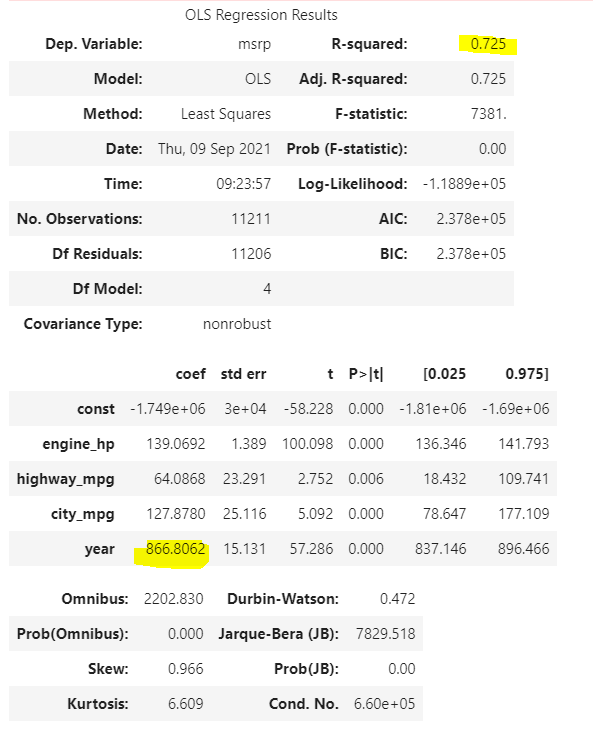
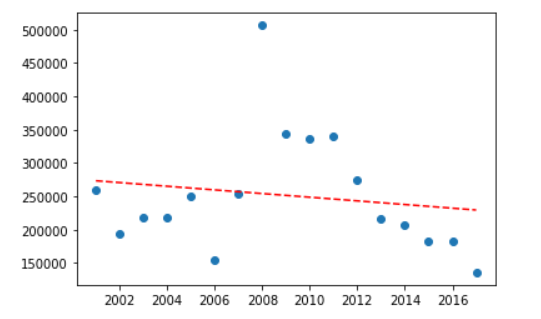
O próximo passo dessa modelagem seria desenvolvermos nossa regressão. O modelo abaixo nos trás duas informações muito importantes. A primeira é de que o modelo é ruim, pois temos um r² de 0,45. A segunda informação, que parece um pouco estranha, é o coeficiente do ano, -562,2877. Isso quer dizer que quanto mais novo o carro, mais barato ele deveria ser.
Vamos analisar mais a fundo. Nos dois gráficos seguintes podemos observar as distribuições do ano do carro e do preço sugerido.
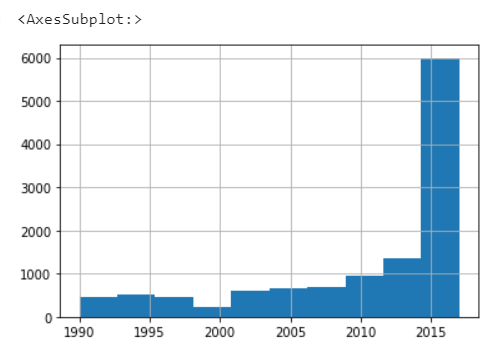
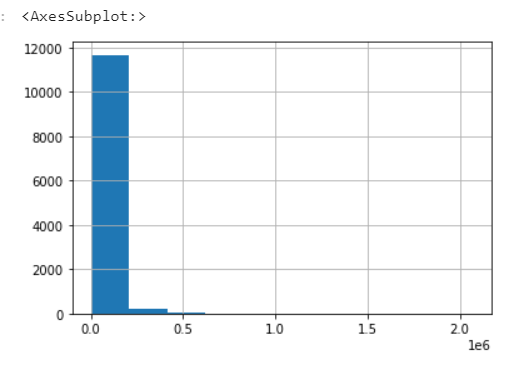
Percebe como elas estão discrepantes? Isso foi exatamente o que o nosso modelo disse, mas sabemos que isso não é uma verdade na maioria dos casos. Então, o que podemos fazer para tornar essa distribuição mais real?
Quando olhamos para a distribuição numérica do valor dos carros, percebemos que 75% custam por volta de R$40.000,00.
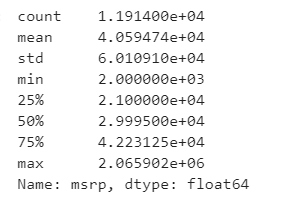
O que deve estar afetando o coeficiente do ano do carro então?
Vamos fazer um teste. Primeiro vamos agrupar os valores sugeridos dos carros por ano e então calcularemos a média. Mas vamos fazer isso olhando em dois recortes, carros que custam menos de 100k e carros que custam mais de 100k.
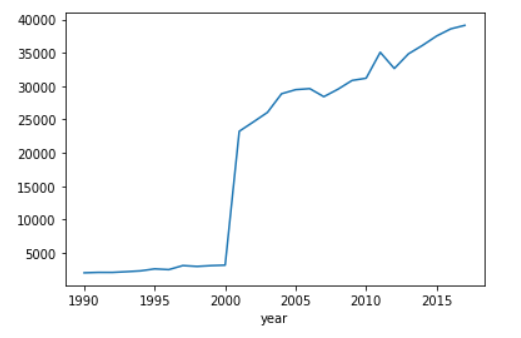
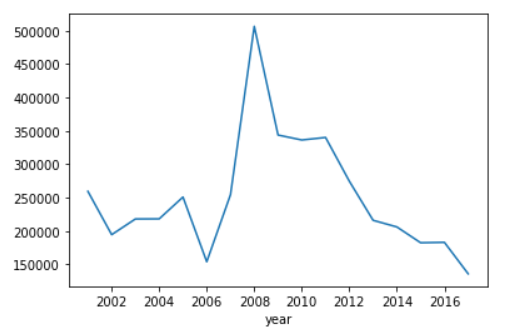
Aqui é possível perceber que a função, para carros que custam menos de 100k, tem um comportamento relativamente linear e crescente.
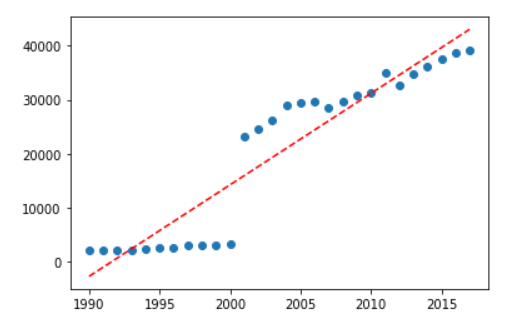
Enquanto carros que custam mais de 100k tem um comportamento não tão linear e é decrescente.
Bom, como quase tudo na vida, nossos dados não seguem um comportamento linear. Assim, nosso modelo de regressão linear atende bem carros que custam menos de R$100.000.
Por tanto, como sugestão, podemos trabalhar com uma base que olhe apenas para carros que custem menos do que R$100.000,00, o que no nosso caso, representa 94,65% da base.
Ao realizarmos a regressão linear para esses modelos, percebemos que nosso r² sobe de 0,45 para 0,725. Outro dado importante é que, agora, nosso coeficiente do ano mudou de -562,2877 para 866,8062, um valor mais condizente com a realidade.
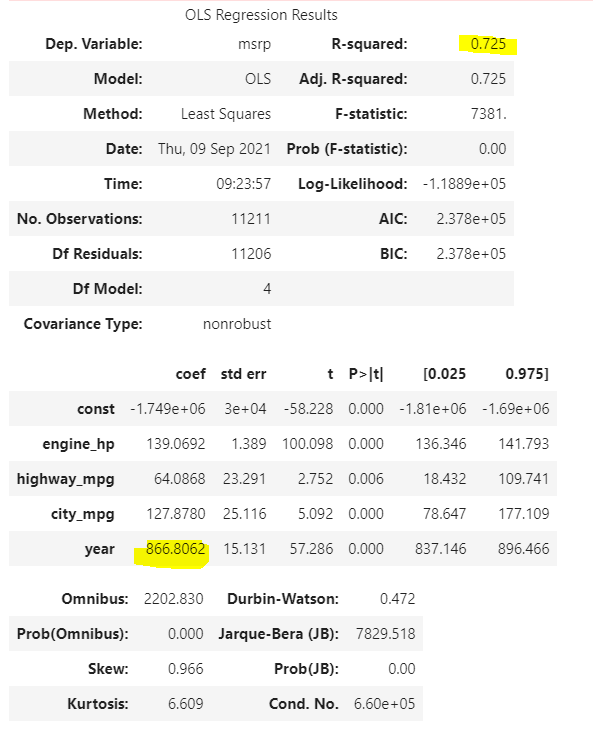
E como ficaria a equação do cálculo do preço do carro então?
Preço sugerido = PS
engine_hp = HP
highway_mph = CE
city_mpg = CC
year = NA
constante = – 1749000
PS = constante + (HP * 139) + (CE * 64) + (CC * 127) + (AN * 866)
Esse modelo ainda pode ser melhorado de várias formas, mas para o nosso propósito didático ele é suficiente.
Conclusões
Assim, percebemos que é possível utilizar ciência de dados nos esportes, na gastronomia e na indústria automobilística. E basicamente, a linha de raciocínio é a mesma. Algumas técnicas podem ser diferentes, assim como o entendimento do próprio negócio. Mas a linha de raciocínio não muda: captamos dados, levantamos hipóteses, transformamos os dados de forma que façam sentido ao negócio, aplicamos modelos estatísticos e matemáticos e finalmente testamos nossas hipóteses. Agora, se é possível aplicar no futebol, no food truck e na indústria automobilística, será que não cabe no seu negócio?
Base de dados utilizada:



