
O desafio de encontrar a verdade oculta nos dados
O que faz data science um campo tão poderoso não é a sua capacidade de lidar com uma enorme quantidade de dados, mas o seu potencial de ver além deles, de interpretar a realidade e descobrir as verdades escondidas atrás dos números. O chamado Paradoxo de Simpson é uma armadilha que mostra a importância da interpretação dos dados em relação ao mundo real. E também aos perigos de simplificar demais uma verdade mais complexa, tentando ver a história toda a partir de um único ponto de vista.
Este fenômeno estatístico ficou conhecido pela descrição feita em um artigo publicado em 1951 por Edward Hugh Simpson, estatístico e criptanalista de Bletchley Park.
O Paradoxo de Simpson diz que uma tendência ou resultado que está presente quando os dados são colocados em grupos, se inverte ou desaparece quando os dados são combinados.
Ou seja: o mesmo conjunto de dados pode parecer mostrar tendências opostas, dependendo de como está agrupado.
Mas o que isso significa e por que é importante?
Exemplo
Um dos exemplos mais famosos do Paradoxo de Simpson é o suspeito preconceito de gênero da UC Berkeley. No início do ano acadêmico em 1973, a escola de pós-graduação da UC Berkeley admitiu cerca de 44% dos candidatos do sexo masculino e 35% do feminino. A escola temia uma ação judicial por discriminação de gênero e pediu ao estatístico Peter Bickel que analisasse os dados. O que ele descobriu foi surpreendente: havia um viés de gênero estatisticamente significativo a favor de mulheres em 4 dos 6 departamentos, e nenhum viés de gênero significativo nos 2 restantes.
A equipe de Bickel descobriu que as mulheres tendiam a se inscrever em departamentos que admitiam uma porcentagem menor de candidatos em geral, e que essa variável oculta afetava os valores marginais para o percentual de inscritos aceitos de forma a reverter a tendência existente no conjunto dos dados.
Essencialmente, a conclusão mudou quando a equipe de Bickel mudou seu ponto de vista sobre os dados para explicar a divisão da escola por departamentos.

Um exemplo visual: a tendência geral se inverte quando os dados são agrupados por alguma categoria representada por cores.
O paradoxo de Simpson é um exemplo de como, mesmo com a boa intenção de tomar uma decisão baseada em dados, podemos facilmente incorrer em erros. Afinal, podemos examinar, reagrupar e reamostrar nossos dados o máximo que pudermos, mas há várias conclusões possíveis a partir de diferentes forma de organizar os dados. Portanto, escolher o agrupamento “correto” para tirar nossas conclusões a fim de obter insights e desenvolver estratégias é um problema difícil de resolver. Precisamos saber o que estamos procurando e escolher o melhor ponto de vista que forneça a representação mais justa possível da verdade. E é aí que mora a complexidade.
Um exemplo de negócios
O matemático e cientista da computação Tom Griggs descreve em artigo no Medium um exemplo do mundo dos negócios:
Suponha que estamos no setor de refrigerantes tentando escolher entre dois novos sabores produzidos. Para consultar a opinião dos consumidores, montamos duas tendas de amostragem para cada sabor em uma área movimentada, para perguntar a 1000 pessoas em cada tenda se elas gostaram dos novos sabores.
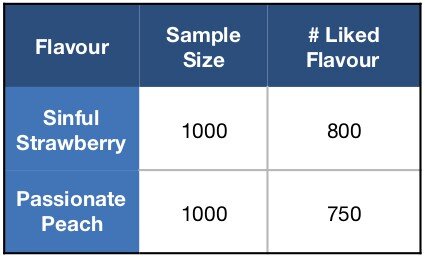
Depois da coleta de informações, podemos ver que 80% das pessoas gostaram do sabor ‘Morango Pecador’, enquanto 75% gostaram do sabor de ‘Pêssego Apaixonado’. Portanto, é mais provável que ‘Morango Pecador’ seja o sabor preferido.
Catálogo de dados conecta todas as fontes de dados e rastreia os armazenamentos de dados para coletar todos os metadados.
Agora, suponha que a equipe coletou algumas outras informações durante a realização da pesquisa, como o sexo da pessoa que experimentou a bebida. O que acontece se dividirmos nossos dados por sexo?
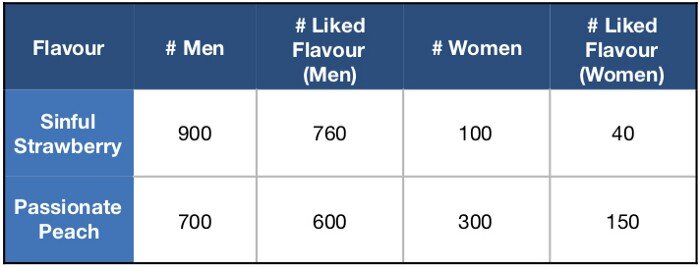
Isso sugere que 84,4% dos homens e 40% das mulheres gostaram de ‘Morango Pecador’, enquanto 85,7% dos homens e 50% das mulheres gostaram de ‘Pêssego Apaixonado’.
Se pararmos para pensar, isso pode parecer um pouco estranho: de acordo com nossos dados de amostra, geralmente as pessoas preferem ‘Morango Pecador’, mas tanto homens quanto mulheres preferem ‘Pêssego Apaixonado’ separadamente. Este é um exemplo do Paradoxo de Simpson!
Nossa intuição nos diz que o sabor que é preferido quando uma pessoa é masculina ou feminina também deve ser preferido quando seu sexo é desconhecido, e é muito estranho descobrir que isso não é verdade – este é o cerne do paradoxo.
Variáveis à espreita
O paradoxo de Simpson surge quando existem variáveis ocultas que dividem os dados em várias distribuições separadas. Essa variável oculta muitas vezes pode ser difícil de identificar.
Uma forma de explicar o paradoxo no exemplo dos refrigerantes é considerar a variável oculta (sexo) e um pouco da teoria da probabilidade:
P (Morango Gostou) = P (Morango Gostou | Homem) P (Homem) + P (Morango Gostou | Mulher) P (Mulher)
800/1000 = (760/900)×(900/1000) + (40/100)×(100/1000)
P (Pêssego Gostou) = P (Pêssego Gostou | Homem) P (Homem) + P (Pêssego Gostou | Mulher) P (Mulher)
750/1000 = (600/700)×(700/1000) + (150/300)×(300/1000)
Podemos pensar nas probabilidades marginais de sexo [P (Homem) e P (Mulher)] como pesos que, no caso de ‘Morango Pecador’, fazem com que a probabilidade total seja significativamente deslocada para a opinião masculina. Embora ainda haja um preconceito masculino oculto em nossa amostra de ‘Pêssego Apaixonado’, ele não é tão forte e, portanto, uma proporção maior da opinião feminina está sendo levada em consideração. Isso resulta em uma probabilidade marginal mais baixa para a população em geral preferir esse sabor, apesar de cada sexo ser mais propenso a preferi-lo quando separado dentro da amostra.
Neste exemplo, as descobertas, no fim das contas, são bastante inconclusivas, pois há compensações na escolha de qualquer um dos pontos de vista, dependendo do objetivo inicial da pesquisa. Porém aqui está o ponto: considerar os agrupamentos e perceber que as descobertas são inconclusivas é mais útil para o negócio do que chegar a uma conclusão errada ou instável. Perceber isso é a coisa certa a fazer para que refazer a pesquisa, buscar novas amostrar e planejar melhor um estudo que dará uma visão mais real.
Por que o paradoxo de Simpson é importante
O Paradoxo de Simpson é importante porque nos lembra que os dados que nos são mostrados não são todos os dados que existem. Não podemos ficar satisfeitos apenas com os números, gráficos ou visualizações instigantes, mas é preciso considerar o processo de geração de dados – o modelo causal – responsável pelos dados.
Uma vez que entendemos o mecanismo de geração dos próprios dados, podemos procurar outros fatores que influenciam um resultado que não estão sendo exibidos na análise de dados, nos impedindo de tirar conclusões erradas ou insuficientes.



